发表于 | 分类于

题目链接

Operation

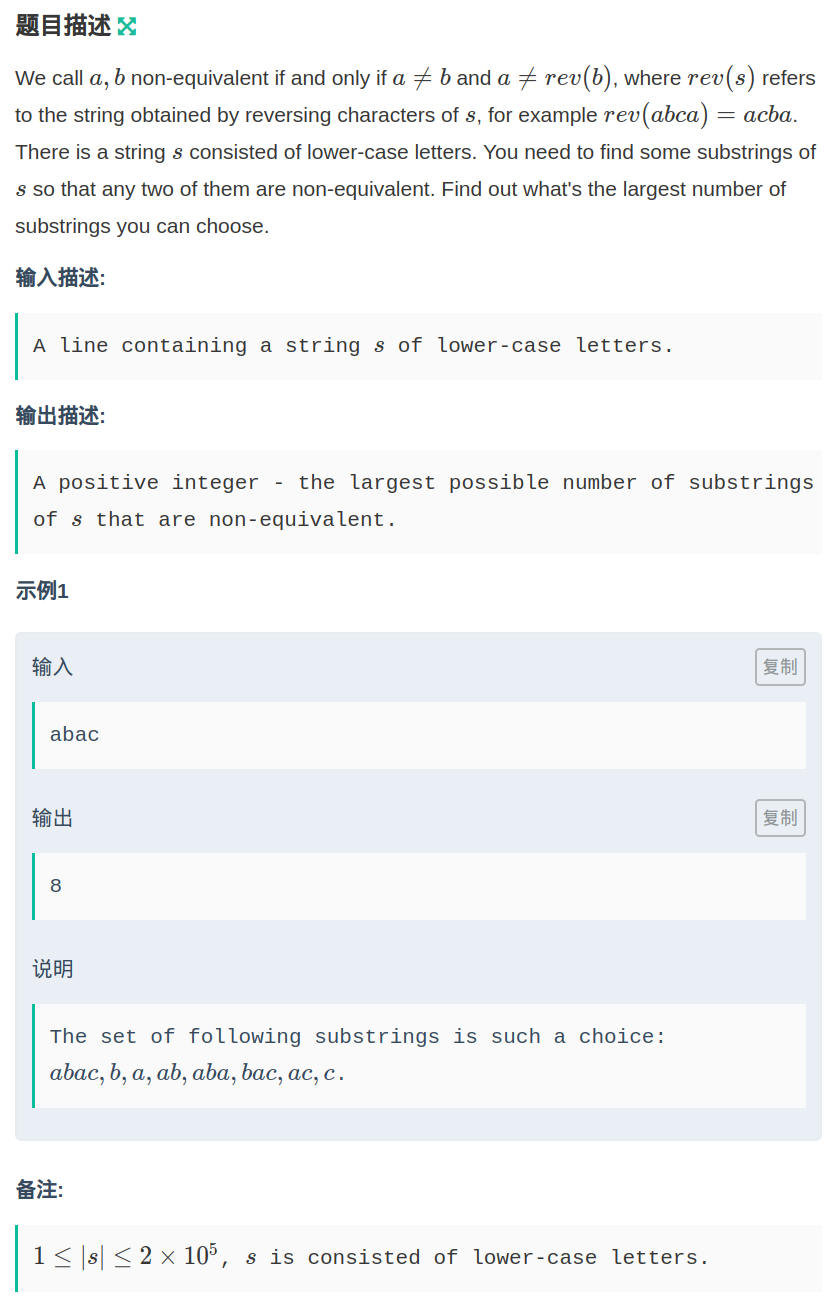
Problem Description

There is an integer sequence a of length n and there are two kinds of operations:

  • 0 l r: select some numbers from al…ar so that their xor sum is maximum, and print the maximum value.

  • 1 x: append x to the end of the sequence and let n=n+1.

Input

There are multiple test cases. The first line of input contains an integer T(T≤10), indicating the number of test cases.
For each test case:
The first line contains two integers n,m$(1≤n≤5×10^5,1≤m≤5×10^5)$, the number of integers initially in the sequence and the number of operations.
The second line contains n integers $a1,a2,…,an(0≤ai<2^{30})$, denoting the initial sequence.
Each of the next m lines contains one of the operations given above.
It’s guaranteed that $∑n≤10^6,∑m≤10^6,0≤x<2^{30}$.
And operations will be encrypted. You need to decode the operations as follows, where lastans denotes the answer to the last type 0 operation and is initially zero:
For every type 0 operation, let l=(l xor lastans)mod n + 1, r=(r xor lastans)mod n + 1, and then swap(l, r) if l>r.
For every type 1 operation, let x=x xor lastans.

Output

For each type 0 operation, please output the maximum xor sum in a single line.

Sample Input

1
3 3
0 1 2
0 1 1
1 3
0 3 4

Sample Output

1
3

题意

给一个长度为n的数组m个操作

  • 0 x y 查询区间$[x,y]$取任意个数能异或出的最大值
  • 1 x 向数组尾部添加一个数x

强制在线

题解

朴素的线性基只能查询1-n能异或出的最大值，这题我们可以保存$[1,n]$每个前缀线性基的状态,查询x,y时只需要查询第y个前缀的线性基就行
但是前缀里会有1-x的线性基影响结果，我们可以在插入线性基时做处理，如果在第pos位上已经有数，且这个数的插入时间比我当前数的插入时间早，那么就把当前要插入的数与该数交换，当前插入时间也交换，直至当前数无法插入或变为0
这样可以让前缀线性基里的数都是越新的，查询的时候判断线性基上数的插入时间是否大于等于x，如果大于x就可以使用这个数。这样处理的正确性是因为线性基插入不受顺序影响，同一组数以不同顺序插入，最后得到的线性基都是等价的

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>

const int mx = 1e6+5;
typedef long long ll;

int sum[mx][32];
int pos[mx][32];
int tot;

void add(int num) {
    ++tot;
    for (int i = 0; i < 32; i++) {
        sum[tot][i] = sum[tot-1][i];
        pos[tot][i] = pos[tot-1][i];
    }

    int now = tot;
    for (int i = 30; i >= 0; i--) {
        if (num & (1<<i)) {
            if (sum[tot][i] == 0) {
                sum[tot][i] = num;
                pos[tot][i] = now;
                break;
            }

            if (now > pos[tot][i]) {
                std::swap(now, pos[tot][i]);
                std::swap(num, sum[tot][i]);  
            }
            num ^= sum[tot][i];
        }
    }
}

int query(int l, int r) {
    int ans = 0;
    for (int i = 30; i >= 0; i--) {
        if (sum[r][i] && pos[r][i] >= l) {
            ans = std::max(ans, ans ^ sum[r][i]);
        }
    }
    return ans;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        int lastans = 0; tot = 0;
        int n, m, num;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &num);
            add(num);
        }

        while (m--) {
            int op, l, r;
            scanf("%d", &op);
            if (op == 0) {
                scanf("%d%d", &l, &r);
                l = (l ^ lastans) % n + 1;
                r = (r ^ lastans) % n + 1;
                if (l > r) std::swap(l, r);
                lastans = query(l, r);
                printf("%d\n", lastans);
            } else {
                scanf("%d", &r);
                add(r ^ lastans);
                n++;
            }
        }
    }
    return 0;
}

发表于 | 分类于

problem

题意

当a != b且a != rev(b)则认为a串与b串不相等，rev(b)表示b串的反串，例如rev(abcd) = dcba
给出一个串求出该串所有不相等的子串个数

题解

先利用后缀数组求出s#rev(s)的不相等子串个数，再扣掉包含字符‘#’的子串个数，包含‘#’的子串个数为$(len(s)+1)^2$,具体取法为以#及左边任意字符为起点，以#及右边字符为终点构成的串，显然这样能取出所有包含#的子串，且这些子串都不相等。
所以求出来结果是$ans = \frac{(2len(s)+1)*(2len(s))}{2}- \sum_{i=2}^{2len(s)+1}height[i]-(len(s)+1)^2$, 这样求出来的结果是包含a = rev(b)的，比如s = abac，求出来的结果是${a,b,c,ab,ba,ac,ca,cab,aba,bac,abac,caba}$,可以看出来除了${a,b,c,aba}$这几个回文串，剩余的串都是成对的，那么我们用回文树求出s本质不同的回文串个数加上之前的ans再除以2就是答案了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#include <bits/stdc++.h>

const int mx = 5e5+5;
typedef long long ll;
char str[mx];

int t1[mx], t2[mx], c[mx];
int sa[mx], rank[mx], height[mx];

bool cmp(int *r, int a, int b, int l) {
    return r[a] == r[b] && r[a+l] == r[b+l];
}

void da(int n, int m) {
    n++;
    int i, j, p, *x = t1, *y = t2;
    for (i = 0; i < m; i++) c[i] = 0;
    for (i = 0; i < n; i++) c[x[i] = str[i]]++;
    for (i = 1; i < m; i++) c[i] += c[i-1];
    for (i = n-1; i >= 0; i--) sa[--c[x[i]]] = i;
    for (j = 1; j <= n; j <<= 1) {
        p = 0;
        for (i = n-j; i < n; i++) y[p++] = i;
        for (i = 0; i < n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;
        for (i = 0; i < m; i++) c[i] = 0;
        for (i = 0; i < n; i++) c[x[y[i]]]++;
        for (i = 1; i < m; i++) c[i] += c[i-1];
        for (i = n-1; i >= 0; i--) sa[--c[x[y[i]]]] = y[i];

        std::swap(x, y);
        p = 1; x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p-1 : p++;
        if (p >= n) break;
        m = p;
    }
    int k = 0;
    n--;
    for (i = 0; i <= n; i++) rank[sa[i]] = i;
    for (i = 0; i < n; i++) {
        if (k) k--;
        j = sa[rank[i]-1];
        while (str[i+k] == str[j+k]) k++;
        height[rank[i]] = k;
    }
}

const int N = 26;
struct pTree {
    int Next[mx][N];
    int fail[mx];
    ll cnt[mx];
    ll sum[mx];
    int num[mx];
    int len[mx];
    int S[mx];
    int last, n, p, cur, now;

    int newnode(int l) {
        for (int i = 0; i < N; i++) Next[p][i] = 0;
        cnt[p] = num[p] = 0;
        len[p] = l;
        return p++;
    }

    void init() {
        n = p = 0;
        newnode(0);
        newnode(-1);
        last = 0;
        S[n] = -1;
        fail[0] = 1;
    }

    int getFail(int x) {
        while (S[n - len[x] - 1] != S[n]) x = fail[x];
        return x;
    }

    bool add(int c) {
        S[++n] = c;
        cur = getFail(last);
        bool flag = false;
        if (!Next[cur][c]) {
            flag = true;
            now = newnode(len[cur] + 2);
            fail[now] = Next[getFail(fail[cur])][c];
            Next[cur][c] = now;
            num[now] = num[fail[now]] + 1;
        }
        last = Next[cur][c];
        cnt[last]++;
        return flag;
    }
    void count() {
        for (int i = p-1; i >= 0; i--) cnt[fail[i]] += cnt[i];
    }
}tree;

int main() {
    scanf("%s", str);
    int len = std::strlen(str);
    str[len] = '#';
    for (int i = len+1; i <= 2*len; i++) str[i] = str[2*len-i];
    str[2*len+1] = '\0';

    int n = 2*len+1;
    da(n, 128);
    ll tot = 1LL * (2*len+1) * (2*len+2)/2;
    tot -= 1LL * (len+1) * (len+1);
    for (int i = 2; i <= n; i++) tot -= height[i];

    tree.init();
    for (int i = 0; i < len; i++) tree.add(str[i]-'a');
    printf("%lld\n", (tot+tree.p-2)/2);
    return 0;
}

发表于 | 分类于

description

题意

求用n个3的倍数的数按位或出数字a的方案数有多少种（0也算3的倍数）

题解

  • 若数b的每个二进制位上的1，在a中也为1，则称b为a的子集
  • 容易知道任意个a的子集按位异或出来的结果还是a的子集
  • 若问题改为按位异或出来的结果是a的子集的方案数，那么答案就是a的子集中是3的倍数的子集个数的n次方
    接着我们对子集按二进制上的1 mod 3的个数划分，例如1101有两个1mod3=1, 一个1mod3 = 2，设$S[i][j]$表示a的子集中有i个mod3=1，j个mod3=2的子集的子集 中是3的倍数的个数，例如a = 1101的一个子集1001表示的状态为$S[1][1]$, 1001的子集中是3的倍数的有1001和0000所以$S[1][1] = 2$，那么$S[i][j]$的n次方就可以表示为用n个3的倍数的数按位或出来的结果的状态是S[i][j]的子集方案数
    那么$\sum_{i=1}^kS[i][k-i]$就表示或出来的结果最多匹配上a中K个1的方案数，那么我们就可以用最多匹配上a中K个1的方案数，减去匹配上a中K-1个1的方案数得出答案，但是这样简单的相减是不行的因为$S[i][k-i]$的子集是会有重叠的，会多扣掉最多匹配k-2个1的方案数，根据容斥原理应当减去最多匹配K-1的方案数，加上最多匹配K-2的方案数，扣掉K-3加上K-4…

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int mx = 65;
const ll mod = 998244353;
int C[mx][mx], S[mx][mx];

ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}

int main() {
    C[0][0] = 1;
    for (int i = 1; i < mx; i++) {
        C[i][0] = 1;
        for (int j = 1; j <= i; j++) {
            C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod;
        }
    }
    
    for (int i = 0; i < mx; i++) {
        for (int j = 0; j < mx; j++) {
            for (int p = 0; p <= i; p++) {
                for (int q = 0; q <= j; q++) {
                    if ((p + 2*q) % 3 != 0) continue;
                    S[i][j] += C[i][p] * C[j][q] % mod;
                    S[i][j] %= mod;
                }
            }
        }
    }
    S[0][0] = 1;

    int T;
    scanf("%d", &T);

    while (T--) {
        ll n, a, x = 0, y = 0;
        scanf("%lld%lld", &n, &a);
        for (int i = 0; i < 64; i++) {
            if (a & (1LL<<i)) {
                if (i % 2 == 0) x++;
                else y++;
            }
        }
        ll ans = 0;
        for (int i = 0; i <= x; i++) {
            for (int j = 0; j <= y; j++) {
                ll tmp = C[x][i] * C[y][j] % mod * pow_mod(S[i][j], n) % mod;
                if ((x+y-i-j) % 2) tmp *= -1;
                ans = (ans + tmp) % mod;
            }
        }
        ans = (ans + mod) % mod;
        printf("%lld\n", ans);
    }
    return 0;
}

发表于 | 分类于

题意

给出一张无向图，定义S[x]表示与点x直接相连的点集，有两个操作
1 x y表示将第x到第y条边状态变化(若存在则删除，不存在则建立)
2 x y询问S[x]与S[y]是否相等

题解

有一个技巧可以压缩的表示点集：给每个点随机一个key，S[x]就可以表示为
与x相连的点的key亦或起来。
考虑如何维护S[x], 因为修改操作是对输入的顺序的区间修改，我们就按边输入的
顺序进行分块，用sum[i][j]记录第i块对点j的贡献值，也就是如果第i块有一条边u-v
那么$sum[i][u] \bigoplus= key[v], sum[i][v] \bigoplus= key[u]$
查询一个点的点集就变成求$sum[1][x] \bigoplus sum[2][x] \bigoplus sum[3][x] \cdots \bigoplus sum[num][x]$
修改的时候如果修改区间落在不同的块上，对夹在中间的块打个lazy标记，表示查询的时候
不用亦或上这个块的贡献，对与两边块内的修改操作可以再用一个数组S记录暴力修改的状态，
比如要修改区间$[l,r]$是块内的,那么就修改$S[u[i]] \bigoplus= key[v[i]], S[v[i]] \bigoplus= key[u[i]] (i\in[l,r])$
查询x的点集时再xor上S[x]就行，总的来说就是块间修改只需要对sum打标记，块内修改就
暴力更改S,最后复杂度$O(q\sqrt m)$，分块的时候块数要开成$1.5\sqrt m$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>

using namespace std;
const int mx = 2e5+10;
typedef long long ll;

int belong[mx], block, num, l[mx], r[mx], id[mx];
int n, m, q, u[mx], v[mx];
int lazy[mx];
ll  sum[450][mx], S[mx];

void build() {
    block = 1.5*sqrt(m);
    num = m / block;
    if (m % block) num++;
    for (int i = 1; i <= num; i++) {
        l[i] = (i-1) * block + 1;
        r[i] = i * block;
        lazy[i] = 1;
        for (int j = 1; j <= n; j++)
            sum[i][j] = 0;
    }
    r[num] = m;
    for (int i = 1; i <= m; i++)
        belong[i] = (i-1) / block + 1;
    for (int i = 1; i <= n; i++) S[i] = 0;
         
}

void update(int x, int y) {
    if (belong[x] == belong[y]) {
        for (int i = x; i <= y; i++) {
            S[u[i]] ^= id[v[i]];
            S[v[i]] ^= id[u[i]];
        }
        return;
    }
    int L = belong[x], R = belong[y];
    for (register int i = x; i <= r[L]; i++) {
        S[u[i]] ^= id[v[i]];
        S[v[i]] ^= id[u[i]];
    }
    for (register int i = L+1; i < R; i++) lazy[i] ^= 1;
    for (register int i = l[R]; i <= y; i++) {
        S[u[i]] ^= id[v[i]];
        S[v[i]] ^= id[u[i]];
    }
}


int main() {
    srand(time(NULL));
    for (int i = 1; i < 100005; i++) id[i] = rand() + 1;
    int T;
    scanf("%d", &T);

    while (T--) {
        scanf("%d%d", &n, &m);
        build();
        for (int i = 1; i <= m; i++) {
            scanf("%d%d", &u[i], &v[i]);
            sum[belong[i]][u[i]] ^= id[v[i]];
            sum[belong[i]][v[i]] ^= id[u[i]];
        }
        scanf("%d", &q);
        while (q--) {
            int op, x, y;
            scanf("%d%d%d", &op, &x, &y);
            if (op == 1) {
                update(x, y);
            } else {
                ll ansx = S[x], ansy = S[y];
                for (int i = 1; i <= num; i++) {
                    if (lazy[i]) {
                        ansx ^= sum[i][x];
                        ansy ^= sum[i][y];
                    }
                }
                putchar(ansx==ansy?'1':'0');
            }
        }
        putchar('\n');
    }
    return 0;
}

发表于 | 分类于

problem

题意

设A(n) = n个1,问有多少对i,j使得$A(i^j)\equiv0(modp)$

题解

$A(n) = \frac{10^n-1}{9}$
当9与p互质时$\frac{10^n-1}{9}\%p = (10^n-1)\cdot inv[9] \% p$
移动项得到$10^n\equiv1(modp)$
由欧拉定理当$gcd(10,p) = 1$时$10^{\varphi(p)}\equiv1(modp)$
那么只要找到最小的d使得$10^d\equiv1(modp)$
问题就转化成求有多少对i,j使得$i^j\equiv0(modp)$
求d只需要枚举$\varphi(p)$的因子就好了
对d分解$d = p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}$
固定j，要使$i^j$是d的倍数，那么i一定是$p_1^{\lceil\frac{k_1}{j}\rceil}p_2^{\lceil\frac{k_2}{j}\rceil}\cdots p_n^{\lceil\frac{k_n}{j}\rceil}$的倍数
设$g_j = p_1^{\lceil\frac{k_1}{j}\rceil}p_2^{\lceil\frac{k_2}{j}\rceil}\cdots p_n^{\lceil\frac{k_n}{j}\rceil}$,答案就是$\sum_{j=1}^mg_j$,因为$k_i$不会超过30，
当j大于30时的$g_j$都一样就不用重复计算了
还有一个问题，当p=3时，因为9与3不互质,inv[9]不存在，式子$\frac{10^n-1}{9}\%p \Longleftrightarrow (10^n-1)\cdot inv[9] \% p$
就不成立，需要特判，此时d取3

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
 
using namespace std;
const int mx = 3e5+10;
typedef long long ll;
 
ll pow_mod(ll a, ll b, ll mod) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}
 
ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b /= 2;
    }
    return ans;
}
 
vector <ll> pp, k;
 
int main() {
    int T;
    scanf("%d", &T);
 
    while (T--) {
        ll p, n, m, d;
        scanf("%lld%lld%lld", &p, &n, &m);
        if (p == 2 || p == 5) {
            printf("0\n");
            continue;
        }
        d = p-1;
        for (ll i = 1; i*i <= (p-1); i++) {
            if ((p-1) % i == 0) {
                if (pow_mod(10, i, p) == 1) {
                    d = min(d, i);
                }
                if (pow_mod(10, (p-1)/i, p) == 1) {
                    d = min(d, (p-1)/i);
                }
            }
        }
        if (p == 3) d = 3;
        pp.clear(); k.clear();
        ll ans = 0;
        for (ll i = 2; i*i <= d; i++) {
            if (d % i == 0) {
                int tmp = 0;
                while (d % i == 0) {
                    tmp++;
                    d /= i;
                }
                k.push_back(tmp);
                pp.push_back(i);
            }
        }
        if (d > 1) pp.push_back(d), k.push_back(1);
 
        ll tmp = 1;
        for (int i = 1; i <= min(30LL, m); i++) {
            tmp = 1;
            for (int j = 0; j < pp.size(); j++) {
                ll b = k[j] / i;
                if (k[j] % i != 0) b++;
                tmp *= pow_mod(pp[j], b);
            }
            ans += n / tmp;
        }
        if (m > 30) ans += n / tmp * (m-30);
        printf("%lld\n", ans);
    }
    return 0;
}

发表于 | 分类于

problem

题意

二维平面上有n个整数坐标的点，求出一条直线将平面上的点分为数量相等的两部分，且线上不能有点，输出线上两个点确定该直线

题解：

先在左下角无穷远处取一质数坐标点(x,y) 对该点和n个点进行极角排序，设排序后中点坐标为(a,b)则这两点连线会将点分为数量相等的两部分，接着取左下角关于中点的对称点(a+a-x, b+b-y),再将该点左移动一格变成(2a-x-1, 2b-y)
则(x,y) (2a-x-1, 2b-y)两点确定的直线就可以分割点为两部分，且线上不会有点

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX=100005;
const int INF=999999;
typedef long long ll;

int n,top;
struct Node
{
       ll x,y;
}p[MAX],S[MAX];
ll Cross(Node a,Node b,Node c)
{
       return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
  
ll dis(Node a,Node b)
{
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
 bool cmp(Node a,Node b)
{  
   ll flag = Cross(p[1],a,b);
   if(flag != 0) return flag > 0;
   return dis(p[1],a) < dis(p[1],b); 
}
  
int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int n;
        scanf("%d", &n);
        p[1].x = -400000009; p[1].y = -2e3;
 
        for(int i=1;i<=n;i++)
            scanf("%lld%lld",&p[i+1].x,&p[i+1].y);
        n++;
        sort(p+2, p+1+n, cmp);
         
        int pos = n/2 + 1;
        ll a = p[pos].x - p[1].x + p[pos].x-1;
        ll b = p[pos].y - p[1].y + p[pos].y;
 
        printf("%lld %lld %lld %lld\n", p[1].x, p[1].y, a, b);
    }
}

发表于 | 分类于

description

题意

有一个数组a给出数组b,$b[i] = mid(a[i-1], a[i], a[i+1])$,mid是中位数，输出一个符合要求的a数组

题解

有一个结论：如果有解，那么一定可以让每个位置最终的值，是它所能影响到的三个中位数之一
设$dp[i][j][k] (1<=i<=n, 0<=j,k<=3)$表示到求到a的第i位时前i-2位合法，第i位放$b[i-2+j]$,第i-1位放$b[i-3+k]$时是否合法，那么判断dp[i][j][k]合法的条件为$dp[i-1][k][q] (0<q<3)$合法且$mid(b[i-2+j],b[i-1-2+k],b[i-2-2+q]) == b[i-1]$也就是判断a[i],a[i-1],a[i-2]的中位数是否为b[i-1]，注意一下头两个数和尾两个数的边界

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>

using namespace std;
const int mx = 3e5+10;
typedef long long ll;
int a[mx], b[mx];

int dp[mx][3][3];
int pre[mx][3][3][3];

int mid(int a, int b, int c) {
    if (a > b) swap(a ,b);
    if (a > c) swap(a, c);
    if (b > c) swap(b, c);
    return b;
}

void out(int i, int j, int k) {
    if (pre[i][j][k][0] == -1) {
        printf("%d ", b[i-2+j]);
        return;
    }
    out(pre[i][j][k][0], pre[i][j][k][1], pre[i][j][k][2]);
    printf("%d ", b[i-2+j]);
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        int n;
        scanf("%d", &n);
        for (int i = 0; i <= n; i++) {
            memset(dp[i], 0, sizeof(dp[i]));
            memset(pre[i], -1, sizeof(pre[i]));
        }

        for (int i = 1; i <= n-2; i++) scanf("%d", &b[i]);
        dp[1][2][0] = dp[2][1][2] = dp[2][2][2] = true;
        pre[2][1][2][0] = 1; pre[2][1][2][1] = 2; pre[2][1][2][2] = 0;
        pre[2][2][2][0] = 1; pre[2][2][2][1] = 2; pre[2][2][2][2] = 0;

        for (int i = 3; i <= n; i++) {
            for (int j =  0; j < 3; j++) {
                if (i == n && j > 0) continue;
                if (i == n-1 && j > 1) continue;
                for (int p = 0; p < 3; p++) {
                    if (i == n && p > 1) continue;
                    for (int q = 0; q < 3; q++) {
                        if (dp[i-1][p][q] && mid(b[i-2+j], b[i-3+p], b[i-4+q]) == b[i-2]) {
                            dp[i][j][p] = true;
                            pre[i][j][p][0] = i-1;
                            pre[i][j][p][1] = p;
                            pre[i][j][p][2] = q;
                        }
                    }
                }
            }
        }
        bool flag = false;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (dp[n][i][j]) {
                    if (!flag) {
                        out(n, i, j);
                        putchar('\n');
                    }
                    flag = true;
                }
            }
        }
        if (!flag) puts("-1");
    }
    return 0;
}

发表于 | 分类于

题目连接：

http://acm.hdu.edu.cn/showproblem.php?pid=6601

Description

N sticks are arranged in a row, and their lengths are a1,a2,…,aN.

There are Q querys. For i-th of them, you can only use sticks between li-th to ri-th. Please output the maximum circumference of all the triangles that you can make with these sticks, or print −1 denoting no triangles you can make.

Input

There are multiple test cases.

Each case starts with a line containing two positive integers N,Q(N,Q≤10^5).

The second line contains N integers, the i-th integer ai(1≤ai≤10^9) of them showing the length of the i-th stick.

Then follow Q lines. i-th of them contains two integers li,ri(1≤li≤ri≤N), meaning that you can only use sticks between li-th to ri-th.

It is guaranteed that the sum of Ns and the sum of Qs in all test cases are both no larger than 4×10^5.

Output

For each test case, output Q lines, each containing an integer denoting the maximum circumference.

Sample Input

5 3
2 5 6 5 2
1 3
2 4
2 5

Sample Output

13
16
16

Hint

题意

给一个长度为N的数组，Q个询问，(l, r)区间内任三个数能构成的三角形的最大周长

题解：

对于排序好的数组，若想要构成三角形周长最大，肯定从最大的边开始取，且三条边是连续的，也就是先取第一大第二大第三大，若不能构成三角形则取第二大第三大第四大，依次取下去。
未排序的数组可以用主席数查询第K大，对于每次询问最多只要查询四十多次，因为若要构造出不能构成三角形的数组，最优构造策略是斐波那契数列，1,2,3,5,8,11,19，到四十多项就超过1e9了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int mx = 1e5+5;
typedef long long ll;

int a[mx], root[mx], cnt;
vector <int> v;
struct node {
   int l, r, sum;
}T[mx*40];

int getid(int x) {
   return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
}

void update(int l, int r, int &x, int y, int pos) {
   T[++cnt] = T[y]; T[cnt].sum++; x = cnt;
   if (l == r) return;
   int mid = (l+r) / 2;
   if (mid >= pos) update(l, mid, T[x].l, T[y].l, pos);
   else update(mid+1, r, T[x].r, T[y].r, pos);
}

int query(int l, int r, int x, int y, int k) {
   if (l == r) return l;
   int mid = (l+r) / 2;
   int sum = T[T[y].l].sum - T[T[x].l].sum;
   if (sum >= k) return query(l, mid, T[x].l, T[y].l, k);
   else return query(mid+1, r, T[x].r, T[y].r, k-sum);
}

int main() {
    int n, m;
    while (scanf("%d%d", &n, &m) != EOF) {
        v.clear();  cnt = 0;
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
            v.push_back(a[i]);
        }
        sort(v.begin(), v.end());
        v.erase(unique(v.begin(), v.end()), v.end());
        for (int i = 1; i <= n; i++) update(1, n, root[i], root[i-1], getid(a[i]));
        for (int i = 1; i <= m; i++) {
            int x, y;
            scanf("%d%d", &x, &y);
            bool flag = false;
            int len = y - x + 1;
            for (int j = 1; j <= y-x-1; j++) {
                ll a = v[query(1, n, root[x-1], root[y], len-j+1)-1];
                ll b = v[query(1, n, root[x-1], root[y], len-(j+1)+1)-1];
                ll c = v[query(1, n, root[x-1], root[y], len-(j+2)+1)-1];
                if (b+c > a) {
                    flag = true;
                    printf("%lld\n", a+b+c);
                    break;
                }
            }
            if (!flag) puts("-1");
        }
    }
    return 0;
}

发表于 | 分类于

题目连接：

https://vjudge.net/problem/SPOJ-NSUBSTR

Description

You are given a string S which consists of 250000 lowercase latin letters at most. We define F(x) as the maximal number of times that some string with length x appears in S. For example for string ‘ababa’ F(3) will be 2 because there is a string ‘aba’ that occurs twice. Your task is to output F(i) for every i so that 1<=i<=|S|.

Input

String S consists of at most 250000 lowercase latin letters.

Output

Output |S| lines. On the i-th line output F(i).

Sample Input

ababa

Sample Output

3
2
2
1
1

Hint

题意

求一个关于串的函数F，F[i]表示串中长度为i的子串出现的最多次数

题解：

这题就是求后缀自动机每个点的Right大小，因为每个endpos类表示的是出现次数及位置一样的一类子串，设一个endpos类中的字符串最长
的长度为len[i]，最短为minlen[i], 所以更新时应更新$ F[j] = max(F[j], |Right[i]|) j \in [minlen[i], len[i]] $,但其实不必每个都更新，因为如果长度为n的字符串出现了m次，那么长度为n-1的字符串一定至少出现了m次，及$ F[i] >= F[j] (i < j) $，所以对于每个点只需要更新$ F[len[i]] = max(F[i],|Right[i]|) $，最后从大到小更新一下F就好了。
然后就是求解Right大小，先对所有前缀节点赋1,然后自底向上更新right($ Right[i] = \sum_{edge[i]} Right[j] $),为了保证Right正确需要以拓扑序更新Rgiht，也就是len[i]大的节点先更新，因为len[i] > len[fa[i]]，len越大的节点越靠近parent tree底部

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int mx = 1e6+5;

struct SAM_automaton {
    int Next[mx][26], len[mx], fa[mx];
    int last, tot;
    int newnode() {
        tot++;
        for (int i = 0; i < 26; i++) Next[tot][i] = 0;
        return tot;
    }

    void init() {
        tot = 0;
        last = newnode();
    }

    void add(int c) {
        int p = last;
        int np = last = newnode();
        len[np] = len[p] + 1;
        while (p && !Next[p][c]) {
            Next[p][c] = np;
            p = fa[p];
        }
        if (!p) fa[np] = 1;
        else {
            int q = Next[p][c];
            if (len[q] == len[p] + 1) fa[np] = q;
            else {
                int nq = newnode();
                len[nq] = len[p] + 1;
                fa[nq] = fa[q];
                for (int i = 0; i < 26; i++) Next[nq][i] = Next[q][i];
                fa[q] = fa[np] = nq;
                while (p && Next[p][c] == q) {
                    Next[p][c] = nq;
                    p = fa[p];
                }
            }
        }
    }
}SAM;

char str[mx];
int r[mx], b[mx], id[mx], f[mx];

int main() {
    SAM.init();
    scanf("%s", str);
    int len = strlen(str);
    for (int i = 0; i < len; i++) SAM.add(str[i] - 'a');
    for (int i = 0, p = 1; i < len; i++) {
        int c = str[i] - 'a';
        r[SAM.Next[p][c]]++;
        p = SAM.Next[p][c];
    }
    for (int i = 1; i <= SAM.tot; i++) b[SAM.len[i]]++;
    for (int i = 1; i <= len; i++) b[i] += b[i-1];
    for (int i = 1; i <= SAM.tot; i++) id[b[SAM.len[i]]--] = i;
    for (int i = SAM.tot; i >= 1; i--) r[SAM.fa[id[i]]] += r[id[i]];

    for (int i = 1; i <= SAM.tot; i++) f[SAM.len[i]] = max(f[SAM.len[i]], r[i]);
    for (int i = len-1; i >= 1; i--) f[i] = max(f[i], f[i+1]);
    for (int i = 1; i <= len; i++) printf("%d\n", f[i]);
    return 0;
}

发表于 | 分类于

题目连接：

https://vjudge.net/problem/SPOJ-LCS2

Description

A string is finite sequence of characters over a non-empty finite set Σ.

In this problem, Σ is the set of lowercase letters.

Substring, also called factor, is a consecutive sequence of characters occurrences at least once in a string.

Now your task is a bit harder, for some given strings, find the length of the longest common substring of them.

Here common substring means a substring of two or more strings.

Input

The input contains at most 10 lines, each line consists of no more than 100000 lowercase letters, representing a string.

Output

The length of the longest common substring. If such string doesn’t exist, print “0” instead.

Sample Input

alsdfkjfjkdsal
fdjskalajfkdsla
aaaajfaaaa

Sample Output

2

Hint

题意

求n个串的最长公共子串长度 (2<=n<=10)

题解：

对a串建后缀自动机，其余串在建好的自动机上跑，记录len[i][j]为第i个串与a串在状态j时的最长公共长度，
与上一题只有两个串不同的是，在每个串跑完后要从底向上的对每个状态j的fa更新len，原因是如果b串和a串有公共子串abcde
那么一定也有公共子串{bcde,cde…} 这时如果不更新len[bcde], len[cde]..当下一个串开始匹配时如果c串和a串公共子串最长只有bcde，那么bcde这个答案就漏掉了，因为此时len[2][endpos(bcde)] = 0，而上一题只有两个串时却不用更新，因为既然b串和a串有公共长度abcde，那么bcde一定长于{bcde,cde..}不更新他们是不会影响到答案的，也就是说c串可能没有abcde但是有bcde所以必须更新fa[abcde]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int mx = 1e6+5;

struct SAM_automaton {
    int Next[mx][26], len[mx], fa[mx];
    int last, tot;
    int newnode() {
        tot++;
        for (int i = 0; i < 26; i++) Next[tot][i] = 0;
        return tot;
    }

    void init() {
        tot = 0;
        last = newnode();
    }

    void add(int c) {
        int p = last;
        int np = last = newnode();
        len[np] = len[p] + 1;
        while (p && !Next[p][c]) {
            Next[p][c] = np;
            p = fa[p];
        }
        if (!p) fa[np] = 1;
        else {
            int q = Next[p][c];
            if (len[q] == len[p] + 1) fa[np] = q;
            else {
                int nq = newnode();
                len[nq] = len[p] + 1;
                fa[nq] = fa[q];
                for (int i = 0; i < 26; i++) Next[nq][i] = Next[q][i];
                fa[q] = fa[np] = nq;
                while (p && Next[p][c] == q) {
                    Next[p][c] = nq;
                    p = fa[p];
                }
            }
        }
    }
}SAM;

char a[mx];
int id[mx], len[12][mx];
int main() {
    SAM.init();
    
    scanf("%s", a);
    int lena = strlen(a);
    
    for (int i = 0; i < lena; i++) SAM.add(a[i]-'a');
    int tot = 0;
    for (int i = 1; i <= SAM.tot; i++) len[tot][i] = SAM.len[i];
    
    while (scanf("%s", a) != EOF) {
        lena = strlen(a);
        tot++;
        int nowlen = 0, p = 1;
        for (int i = 0; i < lena; i++) {
            int c = a[i] - 'a';
            if (SAM.Next[p][c]) {
                nowlen++;
                p = SAM.Next[p][c];
            } else {
                while (p && !SAM.Next[p][c]) p = SAM.fa[p];
                if (p == 0) {nowlen = 0, p = 1;}
                else {
                    nowlen = SAM.len[p] + 1;
                    p = SAM.Next[p][c];
                }
            }
            len[tot][p] = max(len[tot][p], nowlen);
        }
        for (int i = SAM.tot; i >= 1; i--) {
            if (len[tot][i]) {
                for (int j = SAM.fa[i]; j && len[tot][j] != SAM.len[j]; j = SAM.fa[j])//如果len[tot][j] == SAM.len[j]说明fa[j]已经更新过
                    len[tot][j] = SAM.len[j];
            }
        }
    }
    int ans = 0;
    for (int i = 1; i <= SAM.tot; i++) {
        int tmp = len[0][i];
        for (int j = 0; j <= tot; j++)
            tmp = min(tmp, len[j][i]);
        ans = max(ans, tmp);
    }
    printf("%d\n", ans);    
    return 0;
}