I-KM and M

发表于 | 分类于

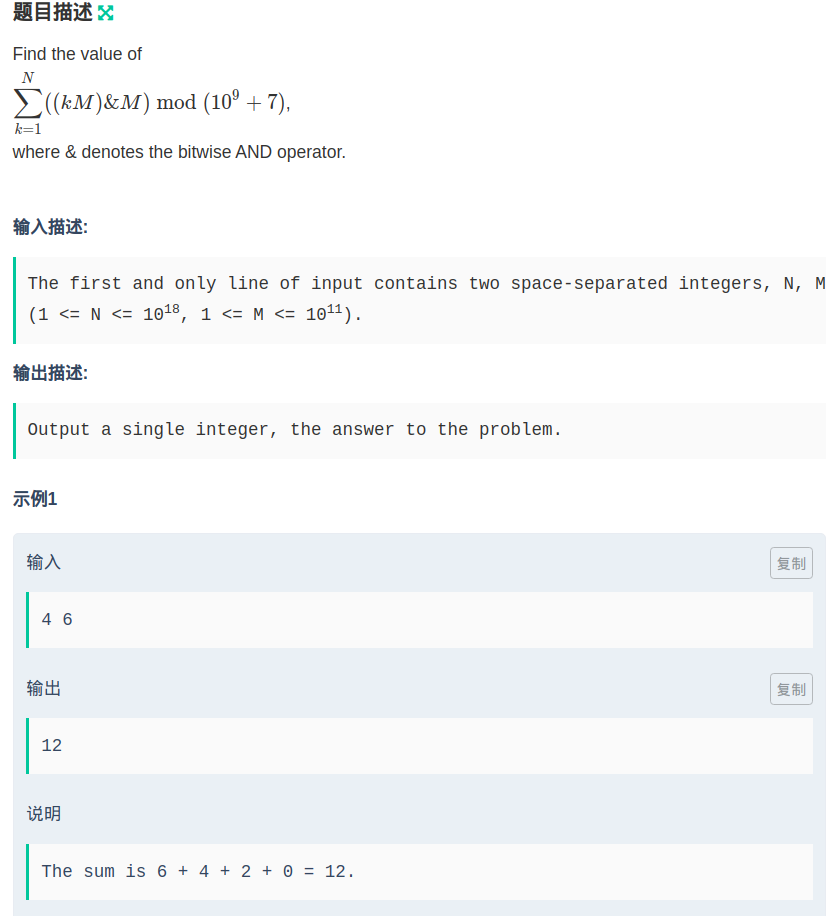
problem

题意

求$\sum_{k=1}^N((kM)\&M) \mod (1e9+7)$

题解

把$\&M$改成$\&$上$M$的每一个二进制位，最后再求和
那么问题就变成求有多少个$kM$在二进制下第x位为1，判断 $kM$在二进制下第x位是否为1可以用$kM \& (1<<x)$判断，但是这样无法快速统计有多少个k满足，我们可以用式子$kM \div 2^x - kM \div 2^{x+1} * 2$是否为1来判断，如果无法理解这个式子可以把除法乘法当成位移运算就容易理解了，那么$\sum_{k=1}^N kM \div 2^x - kM \div 2^{x+1}
* 2$就是$kM$在二进制下第x位为1的方案数了，这个式子可以用类欧几里得算法计算，类欧几里得算法是用来计算$\sum_{i=1}^N \lfloor\frac{a*i+b}{c}\rfloor$的，对应到这题i就是k，a就是M，b为0，c就是$2^x$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
 
ll f(__int128 a, __int128 b,  __int128 c, __int128 n) {
    __int128 m=(a*n+b)/c;
    if(!a || !m)return 0;
    if(a>=c || b>=c)return (n*(n+1)/2%mod*(a/c)%mod+(b/c)*(n+1)%mod+f(a%c,b%c,c,n))%mod;
    return (n*m%mod+mod-f(c,c-b-1,a,m-1)%mod)%mod;
}
 
int main() {
    ll n, m;
    scanf("%lld%lld", &n, &m);
    __int128 ans = 0;
    for (int i = 60; i >= 0; i--) {
        if (m & (1LL<<i)) {
            __int128 cnt = f(m, 0, 1LL<<i, n) - 2*f(m, 0, 1LL<<(i+1), n);
            cnt = (cnt % mod + mod) % mod;
            ans += cnt * (1LL<<i) % mod;
            ans = (ans % mod + mod) % mod;
        }
    }
    ll res = ans % mod;
    printf("%lld\n", res);
    return 0;
}