A-The power of Fibonacci

发表于 | 分类于

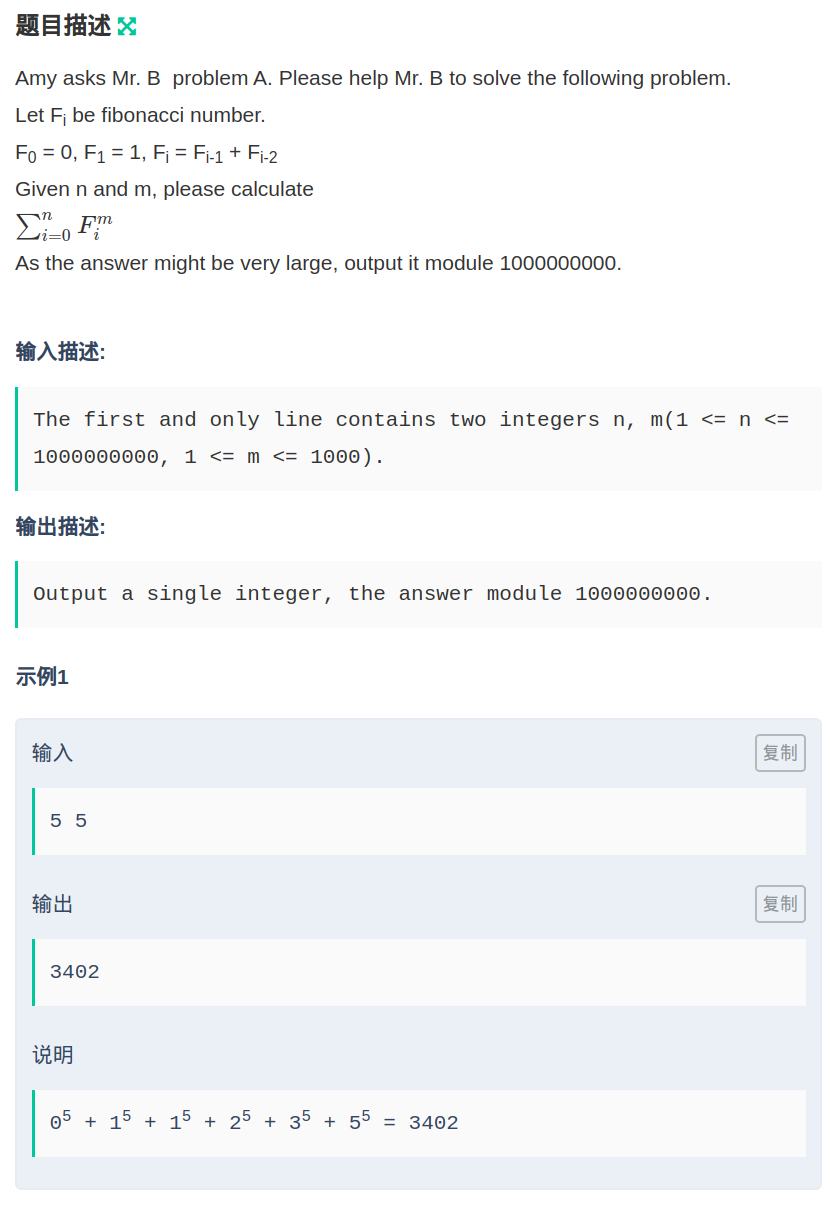
题意

求$\sum_0^n{Fb}_i^m \mod (1e9)$

题解

模1e9时的斐波那契数列循环节太大，考虑把模数质因数分解成$2^9\cdot5^9$，此时循环节变成768和7812500，可以打表预处理，因为$2^9$和$５^9$互质，最后答案可以用中国剩余定理合并

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const int mx = 8e6+5;
int mod[3] = {512, 1953125, 1000000000};
int len[2] = {768, 7812500};
int F[2][mx];
int ans[2][mx];
 
int pow_mod(ll a, ll b, ll p) {
    ll ans = 1;
    while (b) {
        if (b & 1) ans = ans * a % p;
        a = a * a % p;
        b /= 2;
    }
    return ans;
}
 
int main() {
    F[1][0] = F[0][0] = 0;
    F[1][1] = F[0][1] = 1;
     
    for (int k = 0; k < 2; k++) {
        for (int i = 2; i <= len[k]; i++) {
            F[k][i] = (F[k][i-1] + F[k][i-2]);
            if (F[k][i] >= mod[k]) F[k][i] -= mod[k];
        }
    }
    int n, m;
    scanf("%d%d", &n, &m);
    for (int k = 0; k < 2; k++) {
        ans[k][0] = 0;
        for (int i = 1; i <= len[k]; i++) {
            ans[k][i] = (ans[k][i-1] + pow_mod(F[k][i], m, mod[k]));
            if (ans[k][i] >= mod[k]) ans[k][i] -= mod[k];
        }
    }
 
    ll a1 = (ans[0][n%len[0]] + 1LL * ans[0][len[0]-1] * (n/len[0]) % mod[0]) % mod[0];
    ll a2 = (ans[1][n%len[1]] + 1LL * ans[1][len[1]-1] * (n/len[1]) % mod[1]) % mod[1];
    
 
    ll res = a1*mod[1]*109 + a2*mod[0]*1537323;//CRT我直接预处理了   
    res = (res % mod[2] + mod[2]) % mod[2];
    printf("%lld\n", res);
    return 0;
}