I-Median

发表于 | 分类于

description

题意

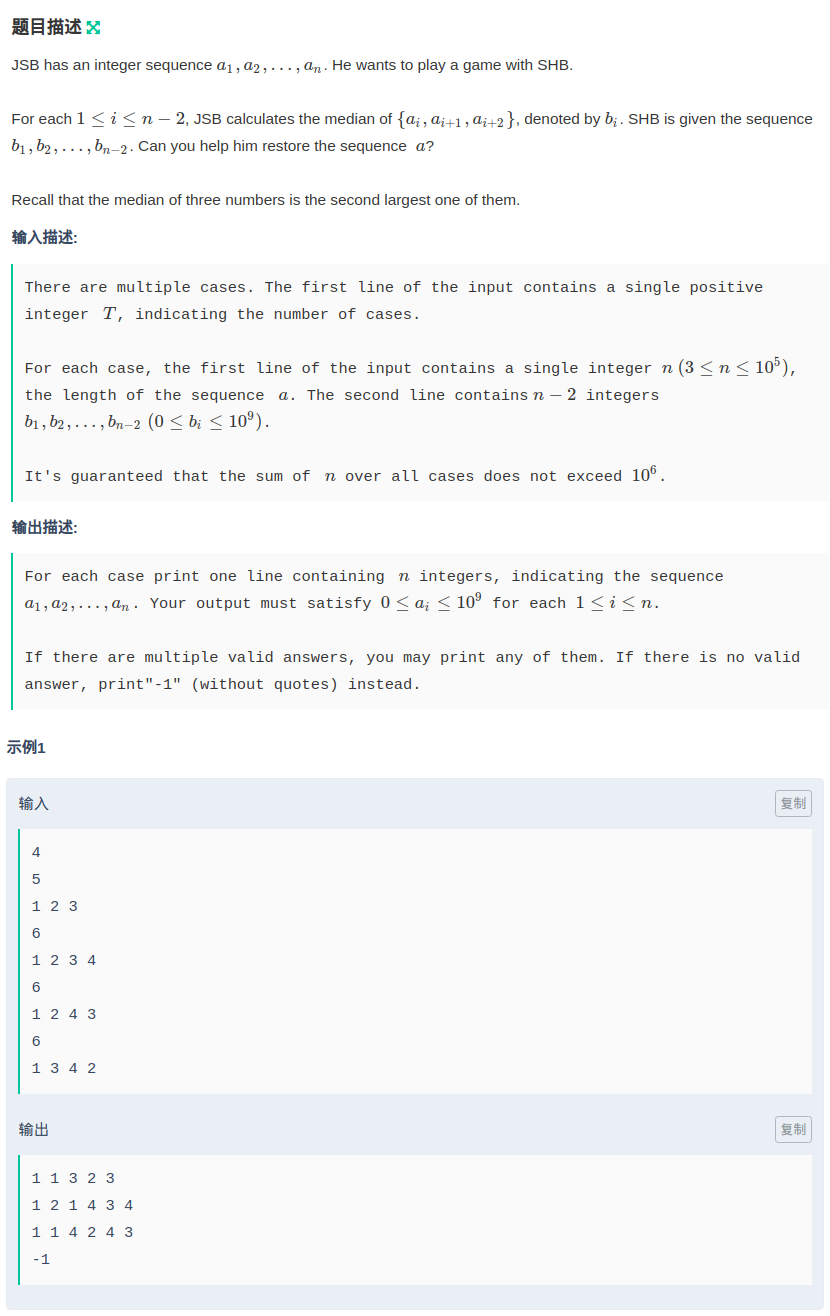
有一个数组a给出数组b,$b[i] = mid(a[i-1], a[i], a[i+1])$,mid是中位数，输出一个符合要求的a数组

题解

有一个结论：如果有解，那么一定可以让每个位置最终的值，是它所能影响到的三个中位数之一
设$dp[i][j][k] (1<=i<=n, 0<=j,k<=3)$表示到求到a的第i位时前i-2位合法，第i位放$b[i-2+j]$,第i-1位放$b[i-3+k]$时是否合法，那么判断dp[i][j][k]合法的条件为$dp[i-1][k][q] (0<q<3)$合法且$mid(b[i-2+j],b[i-1-2+k],b[i-2-2+q]) == b[i-1]$也就是判断a[i],a[i-1],a[i-2]的中位数是否为b[i-1]，注意一下头两个数和尾两个数的边界

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>

using namespace std;
const int mx = 3e5+10;
typedef long long ll;
int a[mx], b[mx];

int dp[mx][3][3];
int pre[mx][3][3][3];

int mid(int a, int b, int c) {
    if (a > b) swap(a ,b);
    if (a > c) swap(a, c);
    if (b > c) swap(b, c);
    return b;
}

void out(int i, int j, int k) {
    if (pre[i][j][k][0] == -1) {
        printf("%d ", b[i-2+j]);
        return;
    }
    out(pre[i][j][k][0], pre[i][j][k][1], pre[i][j][k][2]);
    printf("%d ", b[i-2+j]);
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        int n;
        scanf("%d", &n);
        for (int i = 0; i <= n; i++) {
            memset(dp[i], 0, sizeof(dp[i]));
            memset(pre[i], -1, sizeof(pre[i]));
        }

        for (int i = 1; i <= n-2; i++) scanf("%d", &b[i]);
        dp[1][2][0] = dp[2][1][2] = dp[2][2][2] = true;
        pre[2][1][2][0] = 1; pre[2][1][2][1] = 2; pre[2][1][2][2] = 0;
        pre[2][2][2][0] = 1; pre[2][2][2][1] = 2; pre[2][2][2][2] = 0;

        for (int i = 3; i <= n; i++) {
            for (int j =  0; j < 3; j++) {
                if (i == n && j > 0) continue;
                if (i == n-1 && j > 1) continue;
                for (int p = 0; p < 3; p++) {
                    if (i == n && p > 1) continue;
                    for (int q = 0; q < 3; q++) {
                        if (dp[i-1][p][q] && mid(b[i-2+j], b[i-3+p], b[i-4+q]) == b[i-2]) {
                            dp[i][j][p] = true;
                            pre[i][j][p][0] = i-1;
                            pre[i][j][p][1] = p;
                            pre[i][j][p][2] = q;
                        }
                    }
                }
            }
        }
        bool flag = false;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (dp[n][i][j]) {
                    if (!flag) {
                        out(n, i, j);
                        putchar('\n');
                    }
                    flag = true;
                }
            }
        }
        if (!flag) puts("-1");
    }
    return 0;
}