发表于 | 分类于

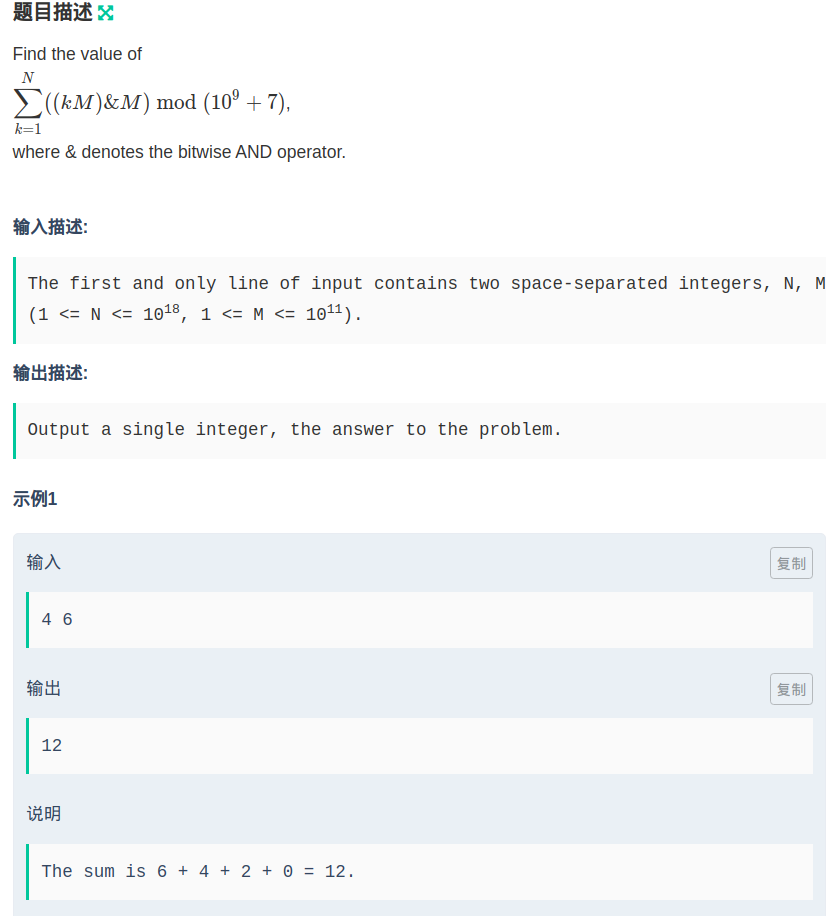
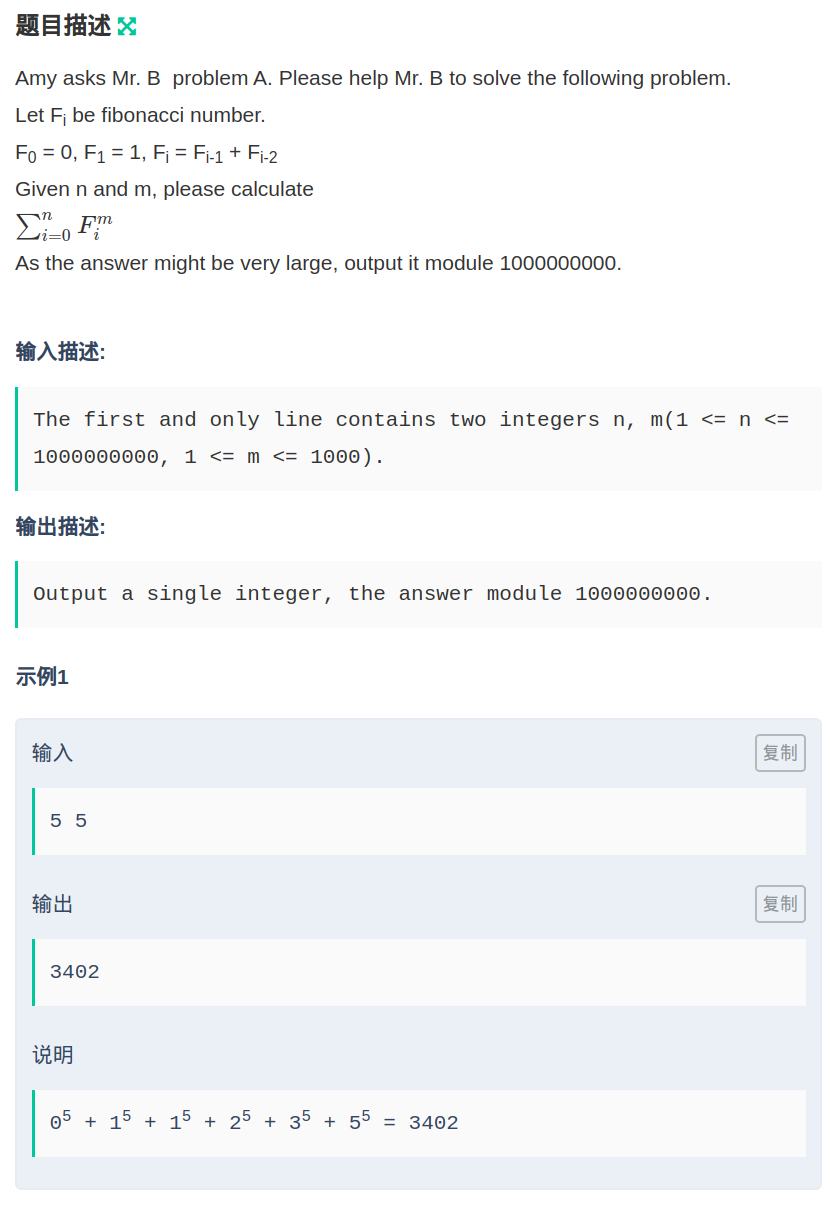
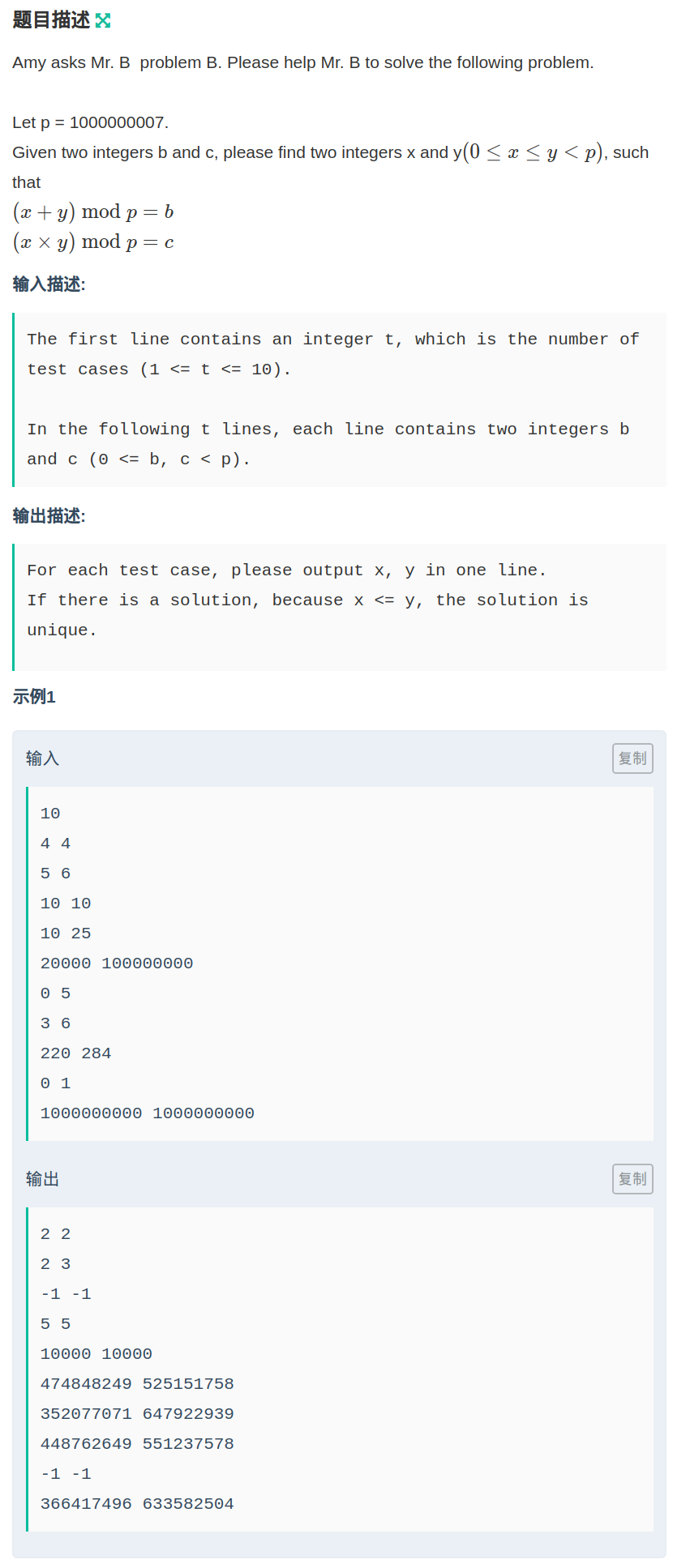
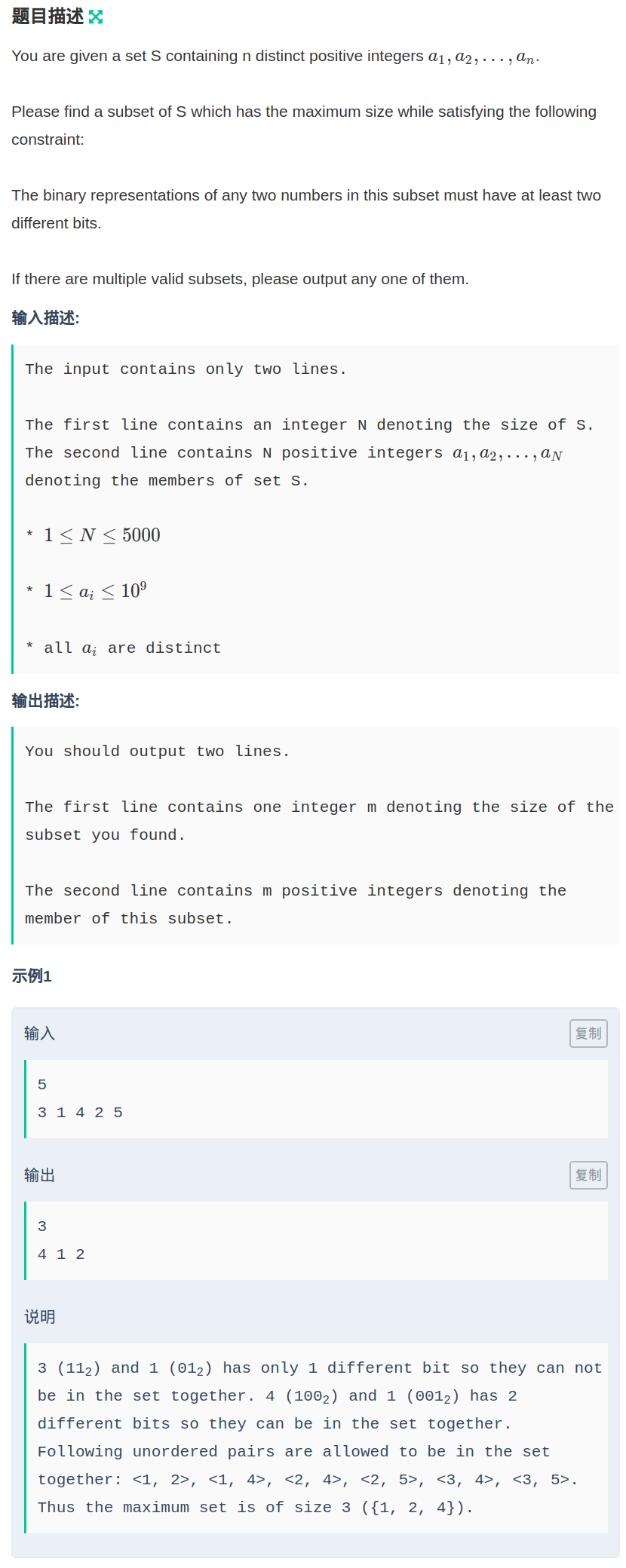
题目链接

hdu-6681

Problem Description

Rikka’s birthday is on June 12th. The story of this problem happens on that day.

Today is Rikka’s birthday. Yuta prepares a big cake for her: the shape of this cake is a rectangular of n centimeters times m centimeters. With the guidance of a grimoire, Rikka is going to cut the cake.

For simplicity, Rikka firstly builds a Cartesian coordinate system on the cake: the coordinate of the left bottom corner is (0,0) while that of the right top corner is (n,m). There are K instructions on the grimoire: The ith cut is a ray starting from (xi,yi) while the direction is Di. There are four possible directions: L, passes (xi−1,yi); R, passes (xi+1,yi); U, passes (xi,yi+1); D, passes (xi,yi−1).

Take advantage of the infinite power of Tyrant’s Eye, Rikka finishes all the instructions quickly. Now she wants to count the number of pieces of the cake. However, since a huge number of cuts have been done, the number of pieces can be very large. Therefore, Rikka wants you to finish this task.

Input

The first line of the input contains a single integer T(1≤T≤100), the number of the test cases.

For each test case, the first line contains three positive integers n,m,K(1≤n,m≤109,1≤K≤105), which represents the shape of the cake and the number of instructions on the grimoire.

Then K lines follow, the ith line contains two integers xi,yi(1≤xi<n,1≤yi<m) and a char Di∈{‘L’,’R’,’U’,’D’}, which describes the ith cut.

The input guarantees that there are no more than 5 test cases with K>1000, and no two cuts share the same x coordinate or y coordinate, i.e., ∀1≤i<j≤K, xi≠xj and yi≠yj.

Output

For each test case, output a single line with a single integer, the number of pieces of the cake.

Hint

The left image and the right image show the results of the first and the second test case in the sample input respectively. Clearly, the answer to the first test case is 3while the second one is 5.

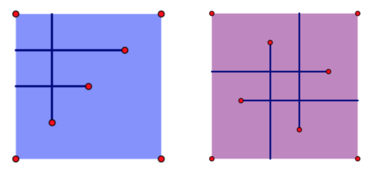
Sample Input

2
4 4 3
1 1 U
2 2 L
3 3 L
5 5 4
1 2 R
3 1 U
4 3 L
2 4 D

Sample Output

3
5

题意

矩形平面上有一些水平或垂直的射线，问这些射线把这个矩形分成了几块

题解

有一个神仙公式叫欧拉公式：$V-E+F=2$，V是点数，E是边数，F是平面数
V = 矩形四个点 + 射线端点n + 射线到矩形交点n + 射线间焦点c = 2n + 4 + c
E = 矩形四条边 + 矩形四条边被射线分割的边n + 射线n条 + 射线与射线分割的边(每个交点都会产生2条新边) 2c
所以F = 2 + c，再扣掉矩形外的平面答案就是1 + c
求交点个数只要从左往右遍历垂直射线，遍历过程中每遇到水平射线左端点则在树状数组上+1，遇到水平射线又端点就在树状数组上-1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
using namespace std;
const int mx = 1e5+5;
int C[mx];
int lowbit(int x) {
    return x & -x;
}
vector <int> vy;
struct Seg {
    int x, y1, y2;
    bool operator < (Seg other) const {
        return x < other.x;
    }
}seg[mx];

struct Point {
    int x, y, val;
    bool operator < (Point other) const {
        return x < other.x;
    }
}point[mx];

int getid(int y) {
    return lower_bound(vy.begin(), vy.end(), y) - vy.begin() + 1;
}

void update(int x, int val) {
    for (int i = x; i < mx; i+=lowbit(i))
        C[i] += val;
}

int query(int l, int r) {
    int sumr = 0, suml = 0;
    for (int i = r; i > 0; i-=lowbit(i)) sumr += C[i];
    for (int i = l-1; i > 0; i-=lowbit(i)) suml += C[i];
    return sumr-suml;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        memset(C, 0, sizeof(C));
        vy.clear();
        
        int n, m, k, x, y;
        int cnts = 0, cntp = 0;
        char dir[2];
        scanf("%d%d%d", &n, &m, &k);
        vy.push_back(0); vy.push_back(m);
        for (int i = 1; i <= k; i++) {
            scanf("%d%d%s", &x, &y, dir);
            vy.push_back(y);
            if (dir[0] == 'L') {
                point[cntp++] = Point{0, y, 1};
                point[cntp++] = Point{x, y, -1};
            } else if (dir[0] == 'R') {
                point[cntp++] = Point{x, y, 1};
                point[cntp++] = Point{n, y, -1};
            } else if (dir[0] == 'U') {
                seg[cnts++] = Seg{x, y, m};
            } else {
                seg[cnts++] = Seg{x, 0, y};
            }
        }
        sort(vy.begin(), vy.end());
        sort(seg, seg+cnts);
        sort(point, point+cntp);
        for (int i = 0; i < cnts; i++) {
            seg[i].y1 = getid(seg[i].y1);
            seg[i].y2 = getid(seg[i].y2);
        }
        for (int i = 0; i < cntp; i++) point[i].y = getid(point[i].y);
        int pos = 0;
        int sum = 0;
        for (int i = 0; i < cnts; i++) {
            while (point[pos].x < seg[i].x) {
                update(point[pos].y, point[pos].val);
                pos++;
            }
            sum += query(seg[i].y1, seg[i].y2);
        }
        printf("%d\n", sum+1);
    }
    return 0;
}

发表于 | 分类于

problem

题意

求$\sum_{k=1}^N((kM)\&M) \mod (1e9+7)$

题解

把$\&M$改成$\&$上$M$的每一个二进制位，最后再求和
那么问题就变成求有多少个$kM$在二进制下第x位为1，判断 $kM$在二进制下第x位是否为1可以用$kM \& (1<<x)$判断，但是这样无法快速统计有多少个k满足，我们可以用式子$kM \div 2^x - kM \div 2^{x+1} * 2$是否为1来判断，如果无法理解这个式子可以把除法乘法当成位移运算就容易理解了，那么$\sum_{k=1}^N kM \div 2^x - kM \div 2^{x+1}
* 2$就是$kM$在二进制下第x位为1的方案数了，这个式子可以用类欧几里得算法计算，类欧几里得算法是用来计算$\sum_{i=1}^N \lfloor\frac{a*i+b}{c}\rfloor$的，对应到这题i就是k，a就是M，b为0，c就是$2^x$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
 
ll f(__int128 a, __int128 b,  __int128 c, __int128 n) {
    __int128 m=(a*n+b)/c;
    if(!a || !m)return 0;
    if(a>=c || b>=c)return (n*(n+1)/2%mod*(a/c)%mod+(b/c)*(n+1)%mod+f(a%c,b%c,c,n))%mod;
    return (n*m%mod+mod-f(c,c-b-1,a,m-1)%mod)%mod;
}
 
int main() {
    ll n, m;
    scanf("%lld%lld", &n, &m);
    __int128 ans = 0;
    for (int i = 60; i >= 0; i--) {
        if (m & (1LL<<i)) {
            __int128 cnt = f(m, 0, 1LL<<i, n) - 2*f(m, 0, 1LL<<(i+1), n);
            cnt = (cnt % mod + mod) % mod;
            ans += cnt * (1LL<<i) % mod;
            ans = (ans % mod + mod) % mod;
        }
    }
    ll res = ans % mod;
    printf("%lld\n", res);
    return 0;
}

发表于 | 分类于

题意

求$\sum_0^n{Fb}_i^m \mod (1e9)$

题解

模1e9时的斐波那契数列循环节太大，考虑把模数质因数分解成$2^9\cdot5^9$，此时循环节变成768和7812500，可以打表预处理，因为$2^9$和$５^9$互质，最后答案可以用中国剩余定理合并

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const int mx = 8e6+5;
int mod[3] = {512, 1953125, 1000000000};
int len[2] = {768, 7812500};
int F[2][mx];
int ans[2][mx];
 
int pow_mod(ll a, ll b, ll p) {
    ll ans = 1;
    while (b) {
        if (b & 1) ans = ans * a % p;
        a = a * a % p;
        b /= 2;
    }
    return ans;
}
 
int main() {
    F[1][0] = F[0][0] = 0;
    F[1][1] = F[0][1] = 1;
     
    for (int k = 0; k < 2; k++) {
        for (int i = 2; i <= len[k]; i++) {
            F[k][i] = (F[k][i-1] + F[k][i-2]);
            if (F[k][i] >= mod[k]) F[k][i] -= mod[k];
        }
    }
    int n, m;
    scanf("%d%d", &n, &m);
    for (int k = 0; k < 2; k++) {
        ans[k][0] = 0;
        for (int i = 1; i <= len[k]; i++) {
            ans[k][i] = (ans[k][i-1] + pow_mod(F[k][i], m, mod[k]));
            if (ans[k][i] >= mod[k]) ans[k][i] -= mod[k];
        }
    }
 
    ll a1 = (ans[0][n%len[0]] + 1LL * ans[0][len[0]-1] * (n/len[0]) % mod[0]) % mod[0];
    ll a2 = (ans[1][n%len[1]] + 1LL * ans[1][len[1]-1] * (n/len[1]) % mod[1]) % mod[1];
    
 
    ll res = a1*mod[1]*109 + a2*mod[0]*1537323;//CRT我直接预处理了   
    res = (res % mod[2] + mod[2]) % mod[2];
    printf("%lld\n", res);
    return 0;
}

发表于 | 分类于

problem

题意

解下列方程
$(x+y) \equiv b \ mod \ p$
$(x\ *\ y) \equiv c \ mod \ p$

题解

$y = b-x$ 带入二式
$x * (b-x) \equiv c \ mod \ p$
$bx - x^2 =c + kp$
$x^2 - bx + c + kp = 0$
解得$x = \frac{b \ \pm \ \sqrt{b^2 - 4c+kp} }{2}$
要使$x$为整数则$\sqrt{b^2 - 4c+kp}$要为整数
令$z = \sqrt{b^2 - 4c+kp}$
$z^2 = b^2 - 4c+kp$
$z^2 \equiv \ b^2 - 4c \ mod \ p$
问题就变成了二次剩余
先判断是否有解也就是$b^2-4c$是否是$p$的二次剩余
利用欧拉准则：当且仅当$d^{\frac{p-1}{2}} \equiv 1 \ mod \ p$，$d$为$p$的二次剩余
当且仅当$d^{\frac{p-1}{2}} \equiv -1 \ mod \ p$，$d$为$p$的非二次剩余
接下来套二次剩余板子求$z$即可，有一种特殊情况当$p \ \% \ 4 = 3$时可以用公式$z = d^{\frac{p+1}{4}} \% \ p$快速求解
现在$x = \frac{b + z}{2}, y = \frac{b - z}{2}$，可能不是整数，我们对x和y都乘上一个偶数(p+1)就可以保证x，y是整数且仍然满足题目的两个方程，因为
$(x+y)*(p+1) \ \%\ p =(x+y) \% p\ *\ (p+1) \% p = b*1 = b$
$x*(p+1)*y*(p+1)\%p = (x*y)\%p\ *\ (p^2+2p+1)\%p = c*1 = c$

*顺带扒了一下咖啡鸡的板子

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
 
ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}
 
int main() {
    int T;
    scanf("%d", &T);
 
    while (T--) {
        ll b, c;
        scanf("%lld%lld", &b, &c);
        ll t = ((b*b - 4*c) % mod + mod) % mod;
        if (pow_mod(t, (mod-1)/2) == mod-1) puts("-1 -1");
        else {
            ll z = pow_mod(t, (mod+1)/4);
            ll x = ((b + z) % mod + mod) % mod;
            ll y = ((b - z) % mod + mod) % mod;
            x = x * (mod+1) / 2 % mod;
            y = y * (mod+1) / 2 % mod;
            if (x > y) swap(x, y);
            printf("%lld %lld\n", x, y);
        }
    }
    return 0;
}

二次剩余模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//调用solve(d, p)返回x
mt19937_64 gen(time(0));
struct T{ll x,y;};
ll w;
T mul_two(T a,T b,ll p){
    T ans;
    ans.x=(a.x*b.x%p+a.y*b.y%p*w%p)%p;
    ans.y=(a.x*b.y%p+a.y*b.x%p)%p;
    return ans;
}
  
T qpow_two(T a,ll n,ll p){
    T ans;
    ans.x=1;
    ans.y=0;
    while(n){
        if(n&1) ans=mul_two(ans,a,p);
        n>>=1;
        a=mul_two(a,a,p);
    }
    return ans;
}
  
ll qpow(ll a,ll n,ll p){
    ll ans=1;
    a%=p;
    while(n){
        if(n&1) ans=ans*a%p;
        n>>=1;
        a=a*a%p;
    }
    return ans%p;
}
  
ll Legendre(ll a,ll p){
    return qpow(a,(p-1)>>1,p);
}
  
int solve(ll n,ll p){
    if (n==0) return 0;
    if (n==1) return 1;
    if(Legendre(n,p)+1==p) return -1;
    ll a,t;
    while(1){
        a=gen()%p;
        t=a*a-n;
        w=(t%p+p)%p;
        if(Legendre(w,p)+1==p) break;
    }
    T tmp;
    tmp.x=a;
    tmp.y=1;
    T ans=qpow_two(tmp,(p+1)>>1,p);
    return ans.x;
}

发表于 | 分类于

problem

题意

N次操作,每次塞入区间$[L,R]$的每个数，并输出此时的中位数。

题解

如果题目不是每次塞入一整个区间，而是只塞入一个数，可以简单的建权值线段树查询区间第K大，由于每次都是查询整个区间就不用主席树了。
现在题目是塞一个区间，那么就要想办法把原来的权值线段树的单点更新变为区间更新，如果L,R的范围较小，可以很容易的把单点修改换成区间修改，题目范围是1e9不可能对整个1e9的区间建树，我们就需要对区间端点进行离散化，原来权值线段树的每一个点的含义由点变成了区间，例如1-5，6-10，离散化为为1-2，3-4，点1就表示1-5这个区间，点3表示6-10这个区间，
但是这样定义点的含义会有一点问题，比如1-5,5-10，离散化为1-2,2-3，此时点1表示1-5，点2表示5-10，点1和点2表示的区间重叠了，那如果我把点含义定义成左闭右开呢？点1表示1-4，点2表示5-9，点10表示10-10，此时如果我想更新1-5这个区间，会发现没法更新，这样定义也不行。
一种做法是把输入的区间右端点+1，比如上面的例子1-5，5-10，变成1-6,5-11，离散化后变成1-3,2-4，点1表示1-4，点2表示5-5，点3表示6-9，点4表示10-10，我要更新1-5只要更新点1和2就行了，问题得到解决。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int mx = 8e5+5;
int x[mx], y[mx];
vector <int> vv;

int getid(int x) {
    return lower_bound(vv.begin(), vv.end(), x) - vv.begin() + 1;
}

struct Tree {
    int lazy, len;
    ll sum;
}tree[mx<<2];

void pushUp(int rt) {
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void pushDown(int rt) {
    tree[rt<<1].lazy += tree[rt].lazy;
    tree[rt<<1|1].lazy += tree[rt].lazy;
    tree[rt<<1].sum += 1LL * tree[rt<<1].len * tree[rt].lazy;
    tree[rt<<1|1].sum += 1LL * tree[rt<<1|1].len * tree[rt].lazy;
    tree[rt].lazy = 0;
}

void build(int l, int r, int rt) {
    if (l == r) {
        tree[rt].len = vv[r+1-1] - vv[l-1];
        tree[rt].sum = tree[rt].lazy = 0;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, rt<<1);
    build(mid+1, r, rt<<1|1);
    tree[rt].len = tree[rt<<1].len + tree[rt<<1|1].len;
}

void update(int L, int R, int l, int r, int rt) { 
    if (L <= l && r <= R) {
        tree[rt].sum += tree[rt].len;
        tree[rt].lazy += 1;
        return;
    }
    int mid = (l + r) / 2;
    pushDown(rt);
    if (L <= mid) update(L, R, l, mid, rt<<1);
    if (mid < R) update(L, R, mid+1, r, rt<<1|1);
    pushUp(rt);
}

int query(int l, int r, ll k, int rt) {
    
    if (l == r) {
        ll t = tree[rt].sum / tree[rt].len;

        return vv[l-1] + (k-1) / t;
    }
    pushDown(rt);
    int mid = (l + r) / 2;
    if (tree[rt<<1].sum >= k) return query(l, mid, k, rt<<1);
    else return query(mid+1, r, k-tree[rt<<1].sum, rt<<1|1);
}

int main() {
    ll n, A1, B1, C1, M1, A2, B2, C2, M2;
    scanf("%lld", &n);
    scanf("%d%d%lld%lld%lld%lld", &x[1], &x[2], &A1, &B1, &C1, &M1);
    scanf("%d%d%lld%lld%lld%lld", &y[1], &y[2], &A2, &B2, &C2, &M2);
    for (int i = 3; i <= n; i++) {
        x[i] = (A1*x[i-1] + B1*x[i-2] + C1) % M1;
        y[i] = (A2*y[i-1] + B2*y[i-2] + C2) % M2;
    }
    for (int i = 1; i <= n; i++) {
        if (x[i] > y[i]) swap(x[i], y[i]);
        x[i]++; y[i]+=2;
        vv.push_back(x[i]);
        vv.push_back(y[i]);
    }
    sort(vv.begin(), vv.end());
    vv.erase(unique(vv.begin(), vv.end()), vv.end());
    vv.push_back(vv[vv.size()-1]+1);
    build(1, vv.size()-1, 1);

    ll sum = 0;
    for (int i = 1; i <= n; i++) {
        update(getid(x[i]), getid(y[i])-1, 1, vv.size()-1, 1);
        sum += y[i]-x[i];
        printf("%d\n", query(1, vv.size()-1, (sum-1)/2+1, 1));
    }
    return 0;
}

发表于

problem

题意

给出n个不同的数字$a_i$，求出最大的子集，使得子集内任意两个数在二进制下至少有两位不同。

题解

先对任意两个二进制位只有一个不同的两个数连边，那么问题就转化成找出最多的点集，任意两点没有边，也就是最大独立集问题。普通的图求最大独立集是N-P困难的，但是二分图求最大独立集合是多项式复杂度的。
所以我们把图转换成二分图形式，把二进制下有奇数个1的数放在左边，有偶数个1的数放在右边，这样左边内的点和右边内的点一定不会有连边，因为两边的点二进制1的个数奇偶性是一样的，且不存在相同的数，那么同一边内的两个数就至少会有两位不同。
接下来就是求二分图的最大独立集，参考博客：二分图的最小顶点覆盖 最大独立集 最大团
简单说就是先用匈牙利求出最大匹配，得到包含在最大匹配内的边，对二分图右边每一个不是最大匹配边的端点的点进行一次dfs，dfs路线是未匹配边->匹配边->未匹配边这样交替，对dfs经过的所有点标记vis。最后二分图左边未标记vis，右边标记了vis的点，就是这张二分图的最大独立集

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const int mx = 5005;
const int INF = 0x3f3f3f3f;
 
vector <int> mp[mx];
vector <int> L, R, ans;
int a[mx], linker[mx];
bool used[mx], vis[mx];
int n;
 
bool dfs(int u) {
    for (int i = 0; i < mp[u].size(); i++) {
        int v = mp[u][i];
        if (!used[v]) {
            used[v] = true;
            if (linker[v] == -1 || dfs(linker[v])) {
                linker[v] = u;
                return true;
            }
        }
    }
    return false;
}
 
int hungary() {
    int res = 0;
    memset(linker, -1, sizeof(linker));
    for (int u = 0; u < L.size(); u++) {
        memset(used, false, sizeof(used));
        if (dfs(L[u])) res++;
    }
    return res;
}
 
void dfs2(int u, int flag) {
    vis[u] = true;
    for (int i = 0; i < mp[u].size(); i++) {
        int v = mp[u][i];
        if (vis[v]) continue;
        if (flag) {
            if (linker[u] != v) dfs2(v, flag^1);
        } else {
            if (linker[v] == u) dfs2(v, flag^1);
        }
    }
}
 
int main() {
    memset(vis, false, sizeof(vis));
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        if (__builtin_popcount(a[i]) % 2 == 1) L.push_back(i);
        else R.push_back(i);
    }
 
    for (int i = 0; i < L.size(); i++) {
        for (int j = 0; j < R.size(); j++) {
            if (__builtin_popcount(a[L[i]]^a[R[j]]) == 1) mp[L[i]].push_back(R[j]), mp[R[j]].push_back(L[i]);
        }
    }
    printf("%d\n", n - hungary());
    for (int i = 0; i < R.size(); i++) {
        int v = R[i];
        //printf("linker[%d] = %d\n", v, linker[v]);
        if (linker[v] == -1) dfs2(v, 1);
    }
    for (int i = 0; i < L.size(); i++)
        if (!vis[L[i]]) ans.push_back(L[i]);
    for (int i = 0; i < R.size(); i++)
        if (vis[R[i]]) ans.push_back(R[i]);
 
    for (int i = 0; i < ans.size(); i++) printf("%d%c", a[ans[i]], i==ans.size()-1?'\n':' ');
    return 0;
}

发表于 | 分类于

problem

题意

给出$x0,x1,a,b$， $x_i = a\cdot x_{i-1} + b\cdot x_{i-2}$，问$x_n取模mod$

题解

用十进制快速幂，二进制快速幂是每到下一位就把a平方，十进制快速幂就是每到下一位就把a变成$a^{10}$，乘10次方的过程再用二进制快速幂优化，总体复杂度就是$O(\log_{10}{n}\cdot \log_2{10})$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int mx = 1e6+5;
ll mod, x0, x1, a, b;
struct mat {
    ll a[2][2];
    mat() {
        clear();
        a[0][0] = 1;
        a[1][1] = 1;
    }
    void clear() {memset(a, 0, sizeof(a));}

    mat operator * (mat other) {
        mat tmp;
        tmp.clear();
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                for (int k = 0; k < 2; k++) {
                    //printf("%d %d %d\n", tmp.a[i][j], a[i][k], other.a[k][j]);
                    tmp.a[i][j] += a[i][k] * other.a[k][j] % mod;
                    tmp.a[i][j] %= mod;
                }
            }
        }
        return tmp;
    }

    mat operator ^ (int y) {
        mat ans = mat();
        mat x = *this;
        while (y > 0) {
            if (y & 1) ans = ans * x;
            x = x * x;
            y /= 2;
        }
        return ans;
    }

    void show() {
        for (int i = 0; i < 2; i++)
            for (int j = 0; j < 2; j++)
                printf("%d%c", a[i][j], j==1?'\n':' ');
    }
};

char str[mx];

int main() {
    scanf("%lld%lld%lld%lld", &x0, &x1, &a, &b);
    scanf("%s%lld", str, &mod);
    mat base;
    base.a[0][0] = a; base.a[0][1] = 1;
    base.a[1][0] = b; base.a[1][1] = 0;
    
    int len = std::strlen(str);
    
    mat res = mat();
    for (int i = len-1; i >= 0; i--) {
        if (str[i] != 0) {
            res = res * (base ^ (str[i]-'0'));
        }
        base = base ^ 10;
    }
    //res.show();
    ll ans = x1 * res.a[0][1] + x0 * res.a[1][1];
    ans = (ans % mod + mod) % mod;
    printf("%lld\n", ans);
    
    return 0;
}

发表于 | 分类于

题目链接

Snowy Smile

Problem Description

There are n pirate chests buried in Byteland, labeled by 1,2,…,n. The i-th chest’s location is (xi,yi), and its value is wi, wi can be negative since the pirate can add some poisonous gases into the chest. When you open the i-th pirate chest, you will get wi value.

You want to make money from these pirate chests. You can select a rectangle, the sides of which are all paralleled to the axes, and then all the chests inside it or on its border will be opened. Note that you must open all the chests within that range regardless of their values are positive or negative. But you can choose a rectangle with nothing in it to get a zero sum.

Please write a program to find the best rectangle with maximum total value.

Input

The first line of the input contains an integer T(1≤T≤100), denoting the number of test cases.

In each test case, there is one integer n(1≤n≤2000) in the first line, denoting the number of pirate chests.

For the next n lines, each line contains three integers xi,yi,wi(−109≤xi,yi,wi≤109), denoting each pirate chest.

It is guaranteed that ∑n≤10000.

Output

For each test case, print a single line containing an integer, denoting the maximum total value.

Sample Input

2
4
1 1 50
2 1 50
1 2 50
2 2 -500
2
-1 1 5
-1 1 1

Sample Output

100
6

题意

平面上有n个点，每个点有价值$w_i$，可以任意选一个矩形，获取矩形内所有点的值，求最大的价值和为多少

题解

先对所有点坐标离散化，枚举矩形上界，对于上界及以下的点，以y坐标相等的点为一组，按y从大到小，一组一组的插入线段树，每插入完一组点，用线段树求出当前的最大子段和，整个过程相当于在枚举矩形上下界，利用线段树维护最大子段和。

线段树每个节点维护：区间和，左端点向右最大子段和，右端点向左最大子段和，区间最大子段和，用类似区间合并的方式合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int mx = 2005;
const ll INF = 1e18;

bool vis[mx][mx];

struct Node {
    int x, y, w;
    int p, q;
}node[mx];

vector <int> vx, vy;
vector <Node> mp[mx];

int getidx(int x) {
    return lower_bound(vx.begin(), vx.end(), x) - vx.begin() + 1;
}

int getidy(int y) {
    return lower_bound(vy.begin(), vy.end(), y) - vy.begin() + 1;
}

struct Tree {
    ll sum;
    ll Lans, Rans, ans;
}tree[mx<<2];

void pushUp(int rt) {
    tree[rt].ans = max(max(tree[rt<<1].ans, tree[rt<<1|1].ans), tree[rt<<1].Rans+tree[rt<<1|1].Lans);
    tree[rt].Lans = max(tree[rt<<1].Lans, tree[rt<<1].sum+tree[rt<<1|1].Lans);
    tree[rt].Rans = max(tree[rt<<1|1].Rans, tree[rt<<1|1].sum+tree[rt<<1].Rans);
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void build(int l, int r, int rt) {
    if (l == r) {
        tree[rt].sum = tree[rt].Lans = tree[rt].Rans = tree[rt].ans = 0;
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, rt<<1);
    build(mid+1, r, rt<<1|1);
    pushUp(rt);
}

void update(int pos, int val, int l, int r, int rt) {
    if (l == r) {
        tree[rt].sum += val;
        tree[rt].Lans = tree[rt].Rans = tree[rt].ans = tree[rt].sum;
        return;
    }
    int mid = (l + r) / 2;
    if (pos <= mid) update(pos, val, l, mid, rt<<1);
    else update(pos, val, mid+1, r, rt<<1|1);
    pushUp(rt);
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        vx.clear(); vy.clear();

        int n;
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d%d%d", &node[i].x, &node[i].y, &node[i].w);
            vx.push_back(node[i].x);
            vy.push_back(node[i].y);
        }
        sort(vx.begin(), vx.end()); sort(vy.begin(), vy.end());
        vx.erase(unique(vx.begin(), vx.end()), vx.end());
        vy.erase(unique(vy.begin(), vy.end()), vy.end());

        for (int i = 1; i <= n; i++) {
            node[i].p = getidx(node[i].x);
            node[i].q = getidy(node[i].y);
        }
        for (int i = 1; i <= vy.size(); i++) mp[i].clear();
        for (int i = 1; i <= n; i++) mp[node[i].q].push_back(node[i]);
        ll ans = 0;
        for (int i = 1; i <= vy.size(); i++) {
            build(1, vx.size(), 1);
            for (int j = i; j <= vy.size(); j++) {
                for (int k = 0; k < mp[j].size(); k++) {
                    Node tmp = mp[j][k];
                    update(tmp.p, tmp.w, 1, vx.size(), 1);
                }
                ans = max(ans, tree[1].ans);
            }
        }
        printf("%lld\n", ans);
    }
    return 0;
}

发表于 | 分类于

题目链接

K-th Closest Distance

Problem Description

You have an array: a1, a2, , an and you must answer for some queries.
For each query, you are given an interval [L, R] and two numbers p and K. Your goal is to find the Kth closest distance between p and aL, aL+1, …, aR.
The distance between p and ai is equal to |p - ai|.
For example:
A = {31, 2, 5, 45, 4 } and L = 2, R = 5, p = 3, K = 2.
|p - a2| = 1, |p - a3| = 2, |p - a4| = 42, |p - a5| = 1.
Sorted distance is {1, 1, 2, 42}. Thus, the 2nd closest distance is 1.

Input

The first line of the input contains an integer T (1 <= T <= 3) denoting the number of test cases.
For each test case:
冘The first line contains two integers n and m (1 <= n, m <= 10^5) denoting the size of array and number of queries.
The second line contains n space-separated integers a1, a2, …, an (1 <= ai <= 10^6). Each value of array is unique.
Each of the next m lines contains four integers L’, R’, p’ and K’.
From these 4 numbers, you must get a real query L, R, p, K like this:
L = L’ xor X, R = R’ xor X, p = p’ xor X, K = K’ xor X, where X is just previous answer and at the beginning, X = 0.
(1 <= L < R <= n, 1 <= p <= 10^6, 1 <= K <= 169, R - L + 1 >= K).

Output

For each query print a single line containing the Kth closest distance between p and aL, aL+1, …, aR.

Sample Input

1
5 2
31 2 5 45 4
1 5 5 1
2 5 3 2

Sample Output

0
1

题意

给出一个数组，m个询问l, r, p,ｋ区间$[l, r]$中$|p-a_i|$第ｋ大的值是多少，ai相同多次计算

题解

二分答案，那么$|p-a_i| \leq ans \Rightarrow p-ans \leq ai \leq p+ans$，利用主席树判断区间$[l,r]$内的$a_i$满足上面限制的数是否大于等于k个，少于k个则增大ans，多于则减小ans，复杂度$O(nlog^2n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int mx = 1e5+5;
typedef long long ll;

int a[mx], root[mx], cnt;
vector <int> v;
struct node {
   int l, r, sum;
}T[mx*40];

int getid(int x) {
   return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
}

void update(int l, int r, int &x, int y, int pos) {
   T[++cnt] = T[y]; T[cnt].sum++; x = cnt;
   if (l == r) return;
   int mid = (l+r) / 2;
   if (mid >= pos) update(l, mid, T[x].l, T[y].l, pos);
   else update(mid+1, r, T[x].r, T[y].r, pos);
}


int query(int l, int r, int x, int y, int k) {
    if (k == 0) return 0;
    if (1 <= l && r <= k) {
        return T[y].sum - T[x].sum;
    }
    int mid = (l + r) / 2;
    int ans = 0;
    if (1 <= mid) ans += query(l, mid, T[x].l, T[y].l, k);
    if (mid < k && mid < r) ans += query(mid+1, r, T[x].r, T[y].r, k);
    return ans;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        v.clear();  cnt = 0;
        int n, m;
        scanf("%d%d", &n, &m);

        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
            v.push_back(a[i]);
        }
        sort(v.begin(), v.end());
        v.erase(unique(v.begin(), v.end()), v.end());
        for (int i = 1; i <= n; i++) update(1, n, root[i], root[i-1], getid(a[i]));

        int l, r, p, k, ans = 0;
        while (m--) {
            scanf("%d%d%d%d", &l, &r, &p, &k);
            l = l^ans;
            r = r^ans;
            p = p^ans;
            k = k^ans;
            int pk = query(1, n, root[l-1], root[r], p);
            int L = 0, R = 0x3f3f3f3f;
            while (L < R) {
                int mid = (L + R) / 2;
                int Lid = getid(p-mid) - 1;
                int Rid = getid(p+mid);
                if (v[Rid-1] != p+mid) Rid--;
                int sum = query(1, n, root[l-1], root[r], Lid) + (r-l+1- query(1, n, root[l-1], root[r], Rid));
                sum = (r-l+1 - sum);
                if (sum >= k) R = mid;
                else L = mid + 1;
            }
            ans = L;
            printf("%d\n", ans);
        }
    }
    return 0;
}

发表于 | 分类于

problem

题意

给出n个数组(每组数个数不定)，m个询问 l, r, x
序号在区间$[l,r]$的每个数组是否都可以取出任意个数异或出x

题解

判断一个数组能否异或出x，是简单的线性基问题
判断多个线性基能否异或出x只需求出这些线性基的交，在交线性基上判断能否异或出x，多个线性基的交一定能被每个线性基分别表示，利用线段树维护区间线性基交就行，线性基求交模板是牛客上扒的咖啡鸡的

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <bits/stdc++.h>
 
using namespace std;
const int mx = 50000+10;
typedef unsigned int ui;
 
ui a[mx][35];
 
struct node{
    ui r[32];
    ui f[32];
    bool ins(ui x){
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) {r[i]=x;return 1;}
                x^=r[i];
                if (!x) return 0;
            }
        return 0;
    }
    void ins2(ui x){
        ui tmp=x;
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) {f[i]=tmp;r[i]=x;return;}
                x^=r[i]; tmp^=f[i];
                if (!x) return;
            }
        return;
    }
    bool find(ui x){
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) return 0;
                x^=r[i];
            }
        return x==0;
    }
    ui calc(ui x){
        ui ret=0;
        for (int i=31;i>=0;i--){
            if (x>>i){
                ret^=f[i];
                x^=r[i];
            }
        }
        return ret;
    }
    void print(){
        for (int i=0;i<3;i++)cout<<r[i]<<' ';cout<<endl;
    }
    void clear(){
        for (int i=0;i<32;i++) r[i]=f[i]=0;
    }
}tree[mx<<2];
 
node merge(node u,node v){
    node ret,tmp;
    ret.clear(); tmp=u;
    for (int i=31;i>=0;i--) {
        ui x=v.r[i];
        if (tmp.find(x)){
            ret.ins(x^tmp.calc(x));
        } else tmp.ins2(x);
    }
    return ret;
}
 
void pushUp(int rt) {
    tree[rt] = merge(tree[rt<<1], tree[rt<<1|1]);
}
 
void build(int l, int r, int rt) {
    if (l == r) {
        for (int i = 1; i <= 32; i++)
            tree[rt].ins(a[r][i]);
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, rt<<1);
    build(mid+1, r, rt<<1|1);
    pushUp(rt);
}
 
bool query(int L, int R, ui x, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return tree[rt].find(x);
    }
    int mid = (l + r) / 2;
    bool f1 = true, f2 = true;
    if (L <= mid) f1 = query(L, R, x, l, mid, rt<<1);
    if (mid < R) f2 = query(L, R, x, mid+1, r, rt<<1|1);
    return f1&&f2;
}
 
int main() {
    int n, m, sz;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &sz);
        for (int j = 1; j <= sz; j++)
            scanf("%u", &a[i][j]);
    }
    build(1, n, 1);
    while (m--) {
        ui l, r, x;
        scanf("%u%u%u", &l, &r, &x);
        puts(query(l, r, x, 1, n, 1) ? "YES" : "NO");
    }
    return 0;
}